×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
物理やら化学やらをやっているといろいろな単位が出てきます。言いたい事は同じなのに、使う単位系が違うせいで全然違った数値になっている事もしばしば。
というわけで、自分用のメモと、数式画像をこしらえてくれるサイトの使い方の練習も兼ねて、原子のイオン化エネルギーのいろいろな表し方を紹介します。
イオン化エネルギーとは、原子(あるいはイオン)の周りにある電子をはぎ取るために必要なエネルギーの事です。電離エネルギー、イオン化ポテンシャル、イオン化電位と呼ばれることもありますが同じ意味です。原子核はプラス、その周囲の電子はマイナスの電荷なのでお互い引き合っていて、それを引き離すために必要なエネルギーというわけです。
中性状態から電子を1個はぎ取って、1価のイオンにするために必要なエネルギーが「第1イオン化エネルギー」、そこから更にもう1個はぎ取って2価のイオンにするために必要なエネルギーが「第2イオン化エネルギー」、以下電子がある限り延々と続きます。まぁ、大抵の場合は「第1イオン化エネルギー」が一番重要なので、第1イオン化エネルギーの事を単に「イオン化エネルギー」と呼ぶ事が多いです。
イオン化エネルギーが大きいという事は電子をはぎ取ってイオン化するのに大きなエネルギーが必要である、つまり電離しにくいということです。逆にイオン化エネルギーが小さければ、電子は比較的小さいエネルギーではぎ取れるので電離しやすいということになります。
周期表の右端にあるヘリウムやネオンなどの希ガス元素は閉殻構造といって電子が安定な配置になっているので、引きはがすにはかなりのエネルギーが必要になります。周期表の左端にあるリチウムやナトリウム、カリウムといった元素の場合は、安定な閉殻構造の一つ外側の電子軌道に1個だけ電子がある状態なので、必要なエネルギーは小さくなります。
さてイオン化エネルギーは、エネルギーと名前が付いている以上当然エネルギーの次元を持つ物理量なわけですが、文献によっていろいろな単位で書いてあります。
例えばネットでイオン化エネルギーを検索するとトップにWikipediaが出てきますが、ここはイオン化エネルギー一覧の単位は[KJ/mol]です。水素の第1イオン化エネルギーは 1312 KJ/mol なので、1molの水素原子全てから1個ずつ電子をはぎ取るのに必要なエネルギーは1312KJである、ということですね。ヘリウムは 2372.3 KJ/mol なので、水素よりも1000KJ以上も余計にエネルギーが必要だと言う事が分かります。次のリチウムはわずか 520.2 KJ/mol なので、非常に電離しやすい元素だと言えます。
[KJ/mol]という単位が示す通り、1molの原子全てから電子を1個ずつはぎ取るのに必要なエネルギーが書いてあるわけですが、原子1molと言ったらものすごい個数になるので、原子1個から電子1個をはぎ取るエネルギーに換算したらものすごく小さなエネルギーになります。
状況によっては、1molの原子がイオン化されるエネルギーよりも、原子1個をイオン化するためのエネルギーの方が知りたいときがあります。その時のイオン化エネルギーを表す単位としてよく使われるのが、[eV]、「電子ボルト(electron volt)」という単位です。
ぱっと見や言葉の響きからするとまるで電圧を表す単位のように思えますが、これもエネルギーを表す単位の一つです。名前が示す通り、電子と電圧が関係しています。
換算を先に書いてしまうと、
1 [eV] = 1.602176565 × 10-19 [J]
となります。
1eVは非常に小さいエネルギーということが分かります。
例えば、水素の第1イオン化エネルギーは約13.6eVです。
イオン化エネルギーが[KJ/mol]で書いてあったり、[eV]で書いてあったりして面倒に思う事があるかもしれませんが、落ち着いて考えてやれば換算は簡単です。
イオン化エネルギーIが [KJ/mol] で書いてある場合は、今は1molをイオン化することなどどうでも良いので、先にmolに消えてもらいます。molというのは物質量の単位で、大雑把に言うと1mol物質があるという事はその中に含まれる原子(あるいは分子、イオンなど)の数は NA (アボガドロ数, 6.0202214129 × 1023) 個あるという事です。
6.0202214129 × 1023個の原子全てから1個ずつ電子をはぎ取るのに必要なエネルギーが I [KJ/mol]ということなので、1個の原子から1個の電子をはぎ取るエネルギーを求めたければ、I [KJ/mol]をアボガドロ数で割ってやります。
こうして出て来た値 I/NA [KJ] は、1個の原子から1個の電子をはぎ取るのに必要なエネルギーになっています。
これを1000倍して単位を[J]にし、1.602176565 × 10-19で割ってやるとめでたく単位が[eV]になります。
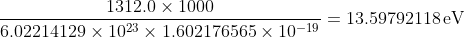
水素のイオン化エネルギーは、電子ボルトに換算すると 13.6 eV であるということが分かります。計算式の有効数字むちゃくちゃですが、その辺は適宜調整を。
1.602176565 × 10-19 [J] ×6.0202214129 × 1023 [/mol] = 96485.33646 [J/mol] = 96.48533646 [KJ/mol] となるので、
例えば、第1イオン化エネルギーは
水素 1312 KJ/mol → 13.60 eV
ヘリウム 2372.3 KJ/mol → 24.59 eV
リチウム 520.2 KJ/mol → 5.39 eV
という換算になります。
うん、理科年表の値ともおおむね一致しているから問題無い。
最後に、ちょっと特殊なイオン化エネルギーの表し方です。
エネルギーの単位は基本的にはジュール[J]で、分野によっては、あるいは古い教科書や参考書ではエルグ[erg]で書かれています。上に挙げたような電子ボルト[eV]もしばしば出てきます。原子や分子など、粒子一つ一つの現象に着目した場合は、電子ボルトを使った方が値がすっきりして表しやすい事が多いです。
しかし、たまにエネルギーが温度に換算されている場合があります。そう表した方が便利なときもあるからそうするわけですが、慣れていないと全くわけが分かりません。そもそもエネルギーと温度では全く次元が異なるので。
温度とエネルギーを換算するには、ボルツマン定数を使います。
kとか、kBとか書かれます。
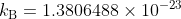
という値です。文献によって小数点第5位くらいから違うこともあります。
このボルツマン定数の次元は [J/K] です。
ボルツマン定数と温度(もちろん℃ではなく、絶対温度[K])はしばしばセットになって現れ、kTでエネルギー[J]の次元になっていることが多いです。つまりボルツマン定数は温度とエネルギーを結びつける役割をしている定数と言えます。
例えば、絶対温度Tのガスの熱エネルギーは大体 kT で表されます。(正しくは係数が付きますが)
この関係を使って、(イオン化エネルギーに限らず)エネルギーを温度で表現する事が出来ます。
あるエネルギーをE [J]としたとき、
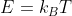
とおいて、
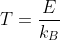
とすると、あるエネルギーE [J]に対応する絶対温度T [K]が計算出来ます。
ボルツマン定数はすごく小さな値なので、1 Jであっても温度換算するととんでもない温度になります。1 Jに対応する温度は、なんと 7.243×1022 K です。
先ほど出て来た電子ボルトを使って、1 eV を温度に換算すると、1.602176565 × 10-19 [J] ÷ k = 11604.5 [K] となります。1 eVに対応する温度はおおよそ1万ケルビンという関係にある事が分かります。
イオン化エネルギーも、ジュールでの値に直してからボルツマン定数で割ってやれば温度で表現することが出来ます。例えば水素のイオン化エネルギーは13.6 eVなので、ジュールにすると2.18×10-18 J です。これをボルツマン定数で割ると157821 K となるので、水素のイオン化エネルギーの温度表現は 157821 K という高い温度であると分かります。
温度とエネルギーの換算はあまり馴染みがありませんがいろいろ使えます。
例えば室温を300 K (= 26.85℃)だとすると、室温をエネルギーに換算すると
k [J/K] ×300 [K] = 4.1419515 × 10-21 [J]
になります。ものすごく小さい値ですが、これを電子ボルトに換算すると
0.0258520... [eV] ≒ 25.85 [meV]
となります。25.85ミリ電子ボルトです。
これは、室温程度の温度の状況下では、空気の各分子が持っているエネルギーは数十ミリ電子ボルトのオーダーであるということを意味します。
(もちろん、正確には係数が付くので少し変わります)
というわけで、自分用のメモと、数式画像をこしらえてくれるサイトの使い方の練習も兼ねて、原子のイオン化エネルギーのいろいろな表し方を紹介します。
イオン化エネルギーとは、原子(あるいはイオン)の周りにある電子をはぎ取るために必要なエネルギーの事です。電離エネルギー、イオン化ポテンシャル、イオン化電位と呼ばれることもありますが同じ意味です。原子核はプラス、その周囲の電子はマイナスの電荷なのでお互い引き合っていて、それを引き離すために必要なエネルギーというわけです。
中性状態から電子を1個はぎ取って、1価のイオンにするために必要なエネルギーが「第1イオン化エネルギー」、そこから更にもう1個はぎ取って2価のイオンにするために必要なエネルギーが「第2イオン化エネルギー」、以下電子がある限り延々と続きます。まぁ、大抵の場合は「第1イオン化エネルギー」が一番重要なので、第1イオン化エネルギーの事を単に「イオン化エネルギー」と呼ぶ事が多いです。
イオン化エネルギーが大きいという事は電子をはぎ取ってイオン化するのに大きなエネルギーが必要である、つまり電離しにくいということです。逆にイオン化エネルギーが小さければ、電子は比較的小さいエネルギーではぎ取れるので電離しやすいということになります。
周期表の右端にあるヘリウムやネオンなどの希ガス元素は閉殻構造といって電子が安定な配置になっているので、引きはがすにはかなりのエネルギーが必要になります。周期表の左端にあるリチウムやナトリウム、カリウムといった元素の場合は、安定な閉殻構造の一つ外側の電子軌道に1個だけ電子がある状態なので、必要なエネルギーは小さくなります。
さてイオン化エネルギーは、エネルギーと名前が付いている以上当然エネルギーの次元を持つ物理量なわけですが、文献によっていろいろな単位で書いてあります。
例えばネットでイオン化エネルギーを検索するとトップにWikipediaが出てきますが、ここはイオン化エネルギー一覧の単位は[KJ/mol]です。水素の第1イオン化エネルギーは 1312 KJ/mol なので、1molの水素原子全てから1個ずつ電子をはぎ取るのに必要なエネルギーは1312KJである、ということですね。ヘリウムは 2372.3 KJ/mol なので、水素よりも1000KJ以上も余計にエネルギーが必要だと言う事が分かります。次のリチウムはわずか 520.2 KJ/mol なので、非常に電離しやすい元素だと言えます。
[KJ/mol]という単位が示す通り、1molの原子全てから電子を1個ずつはぎ取るのに必要なエネルギーが書いてあるわけですが、原子1molと言ったらものすごい個数になるので、原子1個から電子1個をはぎ取るエネルギーに換算したらものすごく小さなエネルギーになります。
状況によっては、1molの原子がイオン化されるエネルギーよりも、原子1個をイオン化するためのエネルギーの方が知りたいときがあります。その時のイオン化エネルギーを表す単位としてよく使われるのが、[eV]、「電子ボルト(electron volt)」という単位です。
ぱっと見や言葉の響きからするとまるで電圧を表す単位のように思えますが、これもエネルギーを表す単位の一つです。名前が示す通り、電子と電圧が関係しています。
換算を先に書いてしまうと、
1 [eV] = 1.602176565 × 10-19 [J]
となります。
1eVは非常に小さいエネルギーということが分かります。
例えば、水素の第1イオン化エネルギーは約13.6eVです。
イオン化エネルギーが[KJ/mol]で書いてあったり、[eV]で書いてあったりして面倒に思う事があるかもしれませんが、落ち着いて考えてやれば換算は簡単です。
イオン化エネルギーIが [KJ/mol] で書いてある場合は、今は1molをイオン化することなどどうでも良いので、先にmolに消えてもらいます。molというのは物質量の単位で、大雑把に言うと1mol物質があるという事はその中に含まれる原子(あるいは分子、イオンなど)の数は NA (アボガドロ数, 6.0202214129 × 1023) 個あるという事です。
6.0202214129 × 1023個の原子全てから1個ずつ電子をはぎ取るのに必要なエネルギーが I [KJ/mol]ということなので、1個の原子から1個の電子をはぎ取るエネルギーを求めたければ、I [KJ/mol]をアボガドロ数で割ってやります。
こうして出て来た値 I/NA [KJ] は、1個の原子から1個の電子をはぎ取るのに必要なエネルギーになっています。
これを1000倍して単位を[J]にし、1.602176565 × 10-19で割ってやるとめでたく単位が[eV]になります。
水素のイオン化エネルギーは、電子ボルトに換算すると 13.6 eV であるということが分かります。計算式の有効数字むちゃくちゃですが、その辺は適宜調整を。
1.602176565 × 10-19 [J] ×6.0202214129 × 1023 [/mol] = 96485.33646 [J/mol] = 96.48533646 [KJ/mol] となるので、
[KJ/mol]での数値 ÷ 96.49 = [eV]での数値
[eV]での数値 × 96.49 = [KJ/mol]での数値
という計算でおおよその換算が出来ることになります。[eV]での数値 × 96.49 = [KJ/mol]での数値
例えば、第1イオン化エネルギーは
水素 1312 KJ/mol → 13.60 eV
ヘリウム 2372.3 KJ/mol → 24.59 eV
リチウム 520.2 KJ/mol → 5.39 eV
という換算になります。
うん、理科年表の値ともおおむね一致しているから問題無い。
最後に、ちょっと特殊なイオン化エネルギーの表し方です。
エネルギーの単位は基本的にはジュール[J]で、分野によっては、あるいは古い教科書や参考書ではエルグ[erg]で書かれています。上に挙げたような電子ボルト[eV]もしばしば出てきます。原子や分子など、粒子一つ一つの現象に着目した場合は、電子ボルトを使った方が値がすっきりして表しやすい事が多いです。
しかし、たまにエネルギーが温度に換算されている場合があります。そう表した方が便利なときもあるからそうするわけですが、慣れていないと全くわけが分かりません。そもそもエネルギーと温度では全く次元が異なるので。
温度とエネルギーを換算するには、ボルツマン定数を使います。
kとか、kBとか書かれます。
という値です。文献によって小数点第5位くらいから違うこともあります。
このボルツマン定数の次元は [J/K] です。
ボルツマン定数と温度(もちろん℃ではなく、絶対温度[K])はしばしばセットになって現れ、kTでエネルギー[J]の次元になっていることが多いです。つまりボルツマン定数は温度とエネルギーを結びつける役割をしている定数と言えます。
例えば、絶対温度Tのガスの熱エネルギーは大体 kT で表されます。(正しくは係数が付きますが)
この関係を使って、(イオン化エネルギーに限らず)エネルギーを温度で表現する事が出来ます。
あるエネルギーをE [J]としたとき、
とおいて、
とすると、あるエネルギーE [J]に対応する絶対温度T [K]が計算出来ます。
ボルツマン定数はすごく小さな値なので、1 Jであっても温度換算するととんでもない温度になります。1 Jに対応する温度は、なんと 7.243×1022 K です。
先ほど出て来た電子ボルトを使って、1 eV を温度に換算すると、1.602176565 × 10-19 [J] ÷ k = 11604.5 [K] となります。1 eVに対応する温度はおおよそ1万ケルビンという関係にある事が分かります。
イオン化エネルギーも、ジュールでの値に直してからボルツマン定数で割ってやれば温度で表現することが出来ます。例えば水素のイオン化エネルギーは13.6 eVなので、ジュールにすると2.18×10-18 J です。これをボルツマン定数で割ると157821 K となるので、水素のイオン化エネルギーの温度表現は 157821 K という高い温度であると分かります。
温度とエネルギーの換算はあまり馴染みがありませんがいろいろ使えます。
例えば室温を300 K (= 26.85℃)だとすると、室温をエネルギーに換算すると
k [J/K] ×300 [K] = 4.1419515 × 10-21 [J]
になります。ものすごく小さい値ですが、これを電子ボルトに換算すると
0.0258520... [eV] ≒ 25.85 [meV]
となります。25.85ミリ電子ボルトです。
これは、室温程度の温度の状況下では、空気の各分子が持っているエネルギーは数十ミリ電子ボルトのオーダーであるということを意味します。
(もちろん、正確には係数が付くので少し変わります)
PR
この記事のトラックバックURL
この記事へのトラックバック

